MATEMATİK ÖĞRENİYORUZ: Mart 2014

18 Mart 2014 Salı

MATRİS VE DETERMİNANT

A. MATRİSİN TANIMI

şeklinde, bir cismin elemanlarının sıralı bir tablosuna m ´ n türünde (m tane satır ve n tane sütun) bir matris denir.

Matrisler büyük harfle gösterilir. Tablodaki yatay sıralara satır, düşey sıralara

sütun adı verilir.

elemanları, A matrisinin 1. satırını oluşturmaktadır.

elemanları, A matrisinin 3. sütununu oluşturmaktadır.

Burada a_ij genel terimi gösterir. i, satır numarası ve j, sütun numarasıdır.

Bu matrisin m kadar satırı, n kadar sütunu vardır.

B. MATRİS ÇEŞİTLERİ

1. Sıfır Matrisi

Bütün elemanları sıfır olan matrise sıfır matrisi denir.

2. Kare Matrisi

Satır ve sütun sayısı eşit olan matrise kare matris denir.

A matrisi (4 ´ 4 boyutlu) 4 satırlı ve 4 sütunlu bir kare matristir.

3. Birim Matris

Bütün köşegen elemanları 1 ve diğer bütün elemanları sıfır olan kare matrislere birim matris denir ve birim matris I harfi ile gösterilir. Yandaki matris 4 ´ 4 boyutlu birim matristir.

C. MATRİSLERİN EŞİTLİĞİ

Aynı türden iki matrisin, bütün aynı indisli terimleri eşit ise, bu matrisler eşittir. Bu ifadenin tersi de doğrudur. Yani, eşit iki matrisin, aynı indisli bütün terimleri eşittir.

D. MATRİSİN DEVRİĞİ (TRANSPOZU)

Bir matrisin devriği (transpozu) satırların sütun, sütunların satır haline getirilmesiyle elde edilen matristir.

Bir A matrisinin transpozu A^T ya da A^d biçimlerinden biri ile gösterilebilir.

E. MATRİSİN REEL SAYI İLE ÇARPIMI

Bir matris c gibi bir sayı ile çarpılınca matrisin bütün elemanları c ile çarpılır.

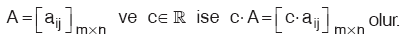
F. MATRİSLERİN TOPLAMI

Aynı türden matrisler toplanır. Bunun için, aynı indisli terimler toplanır.

G. MATRİSLERİN FARKI

Aynı türden matrisler çıkarılır. Bunun için, aynı indisli terimler çıkarılır.

Özellik

1. A + B = B + A (Değişme özelliği vardır.)

2. A + (B + C) = (A + B) + C (Birleşme özelliği vardır.)

3. A + O = O + A = A (Sıfır matrisi toplamaya göre birim (etkisiz) elemandır.)

4. A + (–A) = O (–A matrisi A matrisinin toplamaya göre tersidir.)

5. (A + B)^T = A^T + B^T

6. (A – B)^T = A^T – B^T

7. k × (A + B) = k × A + k × B

8. k × (A – B) = k × A – k × B

9. (k + p) × A = k × A + p × A

10. k × (p × A) = (k × p) × A

H. İKİ MATRİSİN ÇARPIMI

A ve B matrislerinin çarpılabilmesi için A matrisinin sütun sayısı,
B matrisinin satır sayısına eşit olmalıdır.

m ´ n türünde A matrisi ile n ´ p türünde B matrisinin çarpımı m ´ p türünde olur.

Çarpma işlemi birinci matrisin satırları ile ikinci matrisin sütunları çarpılıp toplanarak yapılır.

Özellik

1. A × B ¹ B × A (Değişme özelliği yoktur. Ancak bazı özel durumlarda eşitlik olabilir.)

A × I = I × A

A^m × Aⁿ = A^{m + n}

A^–1 × A = A × A^–1

2. A × (B × C) = (A × B) × C (Birleşme özelliği vardır.)

3. A × (B + C) = A × B + A × C

(B + C) × A = B × A + C × A

Çarpma işleminin toplama işlemi üzerine sağdan ve soldan

dağılma özelliği vardır.

4. A × B = O ise A = O veya B = O olması gerekmez.

5. A × I = I × A = A (I matrisi çarpmaya göre etkisiz elemandır.)

6. A × B = B ise A = I olması gerekmez.

7. (A × B)^T = B^T × A^T

(A × B × C)^T = C^T × B^T × A^T

I. KARE MATRİSİN KUVVETİ

A bir kare matrisi I birim matris ve m, n pozitif tam sayı olmak üzere, matrisin kuvveti aşağıdaki biçimde ifade edilir.

Ayrıca,

olur.

Birim matrisin bütün kuvvetleri yine birim matristir.

Kural

2 × 2 boyutundaki bazı özel matrislerin büyük kuvvetleri karşımıza çıkabilir.Bu özel durumların başlıcaları şunlardır:

J. MATRİSİN DETERMİNANTI

Determinant, kare matrisleri bir sayıya eşleyen fonksiyondur.

Determinant fonksiyonunun, kare matrisi eşlediği o sayıya matrisin determinantı denir.

A matrisinin determinantı, detA veya |A| biçiminde gösterilir.

|A|, matrislerde mutlak değer anlamına gelmez. |A| sıfır veya negatif de olabilir.

Kural

Türü ne olursa olsun, birim matrisin determinantı 1 dir.

1. Sarrus Kuralı

A = [a_ij]_3×3 biçimindeki matrislerin determinantını bulmak için Sarrus kuralı kullanılır.

3 ´ 3 türündeki bir matrisin determinantı şöyle bulunur:

1. İlk iki satır sırasıyla alta birer defa daha yazılır.

2. Köşegeni oluşturan a₁₁, a₂₂, a₃₃ çarpılır; çarpım sağa yazılır.

3. Köşegenin hemen altındaki a₂₁, a₃₂, a₁₃ çarpılır; çarpım sağa yazılır.

4. Aynı yaklaşımla a₃₁, a₁₂, a₂₃ çarpılır; çarpım sağa yazılır.

5. Sağa yazılan üç çarpımın toplamı T₁ olsun

6. Diğer köşegeni oluşturan a₁₃, a₂₂, a₃₁ çarpılır; çarpım sola yazılır.

7. Diğer köşegenin hemen altındaki a₂₃, a₃₂, a₁₁ çarpılır; çarpım sola yazılır.

8. Aynı yaklaşımla a₃₃, a₁₂, a₂₁ çarpılır; çarpım sola yazılır.

9. Sola yazılan üç çarpımın toplamı T₂ olsun,

10. A matrisinin determinantı: detA = T₁ – T₂ dir.

2. İşaretli Minör (Kofaktör)

Bir kare matriste a_ij elemanının minörü M_ij olsun.

a_ij elemanının işaretli minörü (kofaktörü):

Kural

matrisi verilsin.

Bir matrisin determinantı, bu matrisin herhangi bir satır veya sütun elemanları ile bu elemanların işaretli minörlerinin çarpımlarının toplamına eşittir.

i. satıra göre determinant:

j. sütuna göre determinant:

3. Determinantın Özellikleri

Özellik

Bir satır veya bir sütunun tüm elemanları sıfır olan matrislerin determinantı sıfırdır.

Herhangi iki satır veya iki sütunun elemanları eşit olan matrisin determinantı sıfırdır.

Herhangi iki satır veya iki sütunun elemanları orantılı olan matrisin determinantı sıfırdır.

Herhangi iki satır veya iki sütunun yerleri değişirse determinantının işareti değişir.

Bir kare matrisin determinantı ile transpozunun determinantı eşittir.

Kare matrislerin çarpımlarının determinantı, bu matrislerin determinantları çarpımına eşittir.

det(A × B) = detA × detB

Bir kare matrisin kuvvetinin determinantı, determinantının kuvvetine eşittir.

detAⁿ = (detA)ⁿ

Bir kare matrisin çarpmaya göre tersinin determinantı, determinantının tersine eşittir.

A = [a_ij|_m×n matrisinin k ile çarpımının determinantı,
A nın determinantının kⁿ ile çarpımına eşittir.

Bir kare matrisin bir satır ve bir sütunun tüm elemanları
k ile çarpılırsa, elde edilen matrisin determinantı ilk matrisin determinantının k ile çarpımına eşittir.

Bir matrisin herhangi bir satırını k ile çarpıp diğer bir satıra ekleyince veya herhangi bir sütununu k ile çarpıp diğer bir sütuna ekleyince determinantının değeri değişmez.

Sadece bir satır veya bir sütun elemanları farklı olan matrislerin determinantları toplamı, diğer satır veya sütunları aynı olan ve farklı sütunu farklı sütunların toplamı kadar olan yeni matrisin determinantına eşittir.

K. EK MATRİS (ADJOİNT MATRİS)

Bir matrisin elemanları yerine, o elemanların işaretli minörlerinin yazılıp transpozu alınarak elde edilen matrise ek matris denir ve Ek(A) biçiminde gösterilir.

L. BİR MATRİSİN ÇARPMA İŞLEMİNE GÖRE TERSİ

a = [A_ij]_m×m biçimindeki kare matrislerin, çarpmaya göre tersini A^–1 biçiminde gösteririz.

Determinantı sıfırdan farklı matrislerin tersi vardır.

Kural

Özellik

17 Mart 2014 Pazartesi

AÇI VE AÇI ÇEŞİTLERİ

                                                    AÇI

     Tanım : Başlangıç noktası aynı olan iki ışın açı oluşturur.

Yukarıdaki açı “ABC açısı” , “CBA açısı” veya “B açısı” şeklinde isimlendirilir.

sembollerinden biri ile gösterilebilir.

Açının kenarları arasında kalan bölge açının içi veya iç bölgesidir.

Açı ile açının iç bölgesinin dışında kalan bölge açının dışı veya dış bölgesidir.

Açı üzerindeki noktalar açının iç veya dış bölgesine ait değildir.

ÖRNEK:

A ve B noktaları açının iç bölgesinde, C ve Y noktaları açının dış bölgesindedir.

O, N ve S noktaları açının üzerindedir. N noktası aynı zamanda açının köşesidir.

Tanım: Ölçüleri eşit olan açılara eş açılar denir.

AÇIORTAY

Tanım: Başlangıç noktası açının köşesi olan, açının iç bölgesinde bulunan ve açıyı iki eş

açıya ayıran ışına bu açının açıortayı denir.

ÖRNEK:

[LN ışını KLM açısını iki eş açıya böldüğü için açıortaydır.

KOMŞU AÇILAR

Tanım: Birer kenarı ortak olan iki açıya komşu açılar denir.

Komşu açıların ortak olmayan iki kenarı da farklı bir açı oluşturur.

Yukarıdaki şekle göre bu açı ABC açısıdır.

Komşu açıların iç bölgelerinin ortak noktası yoktur.

TÜMLER AÇILAR

Tanım : Ölçüleri toplamı 90º olan iki açıya tümler açılar denir.

ÖRNEK:

33º lik bir açının tümler açısının ölçüsünün kaç derece olduğunu bulalım.

Tümler açısına “x” dersek 33º + x = 90º

x = 90º - 33º

x = 57º dir.

BÜTÜNLER AÇILAR

Tanım: Açıların ölçüleri toplamı 180º olan iki açıya bütünler açılar denir.

ÖRNEK:

41ºlik açının bütünler açısının ölçüsünün kaç derece olduğunu bulalım.

Bilinmeyen açıya x dersek 41º + x = 180º

x = 180º - 41º

x = 139º olur.

KOMŞU BÜTÜNLER AÇILAR

Tanım: Birer kenarları ortak olan bütünler açılara komşu bütünler açılar denir.

Komşu bütünler açıların bir kenarları ortak, diğer kenarları aynı doğrultuda fakat ters yönde

olduğundan aynı zamanda bir doğrusal çift oluştururlar.

KOMŞU TÜMLER AÇILAR

Tanım: Birer kenarı ortak olan tümler açılara komşu tümler açılar denir.

Not : Bir açının ölçüsü sembolle gösterilirken “s veya m” harflerinden biri kullanılır.

Bir açının kenarlarının kısa veya uzun çizilmesi açının ölçüsünü değiştirmez.

TERS AÇILAR

Not: İki doğrunun kesişmesi ile oluşan karşılıklı açılara ters açılar denir. Ters açıların

ölçüleri birbirine eşittir.

Yukarıdaki kesişen doğrularda AOD ile BOC açıları ters açı olup ölçüleri eşittir. AOB ile COD

açıları da ters açı olup ölçüleri eşittir.

Komşu Açılar: Köşesi ve birer kenarı ortak olan açılar komşu açılar denir. Aşağıdaki örnekte ABC açısı ile CBD açısının BC kenarı ortak olduğu için bu iki açı komşudur.

Kaynak Linki : http://www.matematikciler.org/6-sinif/matematik-konu-anlatimlari/422-acilar-aci-cesitleri-es-acilar-aciortay-komsu-aci.html

Açı Nedir? Başlangıç noktaları aynı olan iki ışının birleşimine açı denir. İki ışının ortak olan başlangıç noktasına açının köşesi denir. Işınlara ise aççının kenarı veya açının kolu denir. Yukarıdaki açı AOB açısı, BOA açısı veya O açısı olarak isimlendirilir. Sembolle AÔB, BÔA veya Ô şeklinde gösterilir. Açının Düzlemde Ayırdığı Bölgeler Açı bulunduğu düzlemi iç ve dış bölge olmak üzere iki bölgeye ayırır. Açının kolları sonsuza uzadığı için kolları kısa veya uzun çizmemiz iç bölgeyi veya dış bölgeyi değiştirmez. Yukarıdaki örnekte D, E ve F noktaları açının iç bölgesinde, H ve G noktaları açının dış bölgesindedir. A, B ve C noktaları ise açının ne iç bölgesinde ne de dış bölgesindedir. Bu noktalar açının üzerindedir. AÇI ÇEŞİTLERİ Açıyı oluşturan iki ışın arasındaki açıklığa açının ölçüsü denir. Açı ölçü birimlerinden birisi derecedir. Örneğin 30 derecelik bir açı 300 şeklinde gösterilir. Bir AOB açısının ölçüsü sembolle s(AÔB) veya m(AÔB) şeklinde gösterilir. 1-Dar Açı: Ölçüsü 00 ile 900 arasında olan açıya dar açı denir. 2-Dik Açı: Ölçüsü 900 olan açıya dik açı denir. 3-Geniş Açı: Ölçüsü 900 ile 1800 arasında olan açıya geniş açı denir. 4-Doğru Açı: Ölçüsü 1800 olan açıya doğru açı denir. 5-Tam Açı: Ölçüsü 3600 olan açıya tam açı denir. Eş Açı: Ölçüleri birbirine eşit olan açılara eş açılar denir. Örneğin s(AÔB)=400 ve s(AÔC)=400 olsun. Bu iki açı birbirine eştir. Bu durum sembolle AÔB @ AÔC şeklinde gösterilir. Açıortay: Bir açıyı iki eş açıya bölen ışına açı ortay denir. Yandaki örnekte DT ışını LDE açısının açıortayıdır. Komşu Açılar: Köşesi ve birer kenarı ortak olan açılar komşu açılar denir. Aşağıdaki örnekte ABC açısı ile CBD açısının BC kenarı ortak olduğu için bu iki açı komşudur.

Kaynak Linki : http://www.matematikciler.org/6-sinif/matematik-konu-anlatimlari/422-acilar-aci-cesitleri-es-acilar-aciortay-komsu-aci.html